Introduction to Statistics for Data Science
- Juan Manuel Ortiz de Zarate

- Aug 20, 2024
- 10 min read
Updated: Aug 21, 2024
The concept of data analysis lies at the core of statistical science, a discipline dedicated to developing and applying methods for gathering, presenting, organizing, and analyzing information. The primary aim of statistics is to equip decision-makers with tools to make informed choices, especially when faced with uncertainty.
Data analysis is an essential process within this broader statistical framework. It involves a systematic approach to exploring, cleaning, and transforming data. The purpose of this process is to uncover meaningful insights that can guide decision-making, suggest possible conclusions, and even forecast future trends. By transforming raw data into actionable information, data analysis enables individuals and organizations to make decisions that are not just based on intuition but are supported by empirical evidence and rigorous examination.
Descriptive statistics and inferential statistics are two fundamental branches of statistical analysis, each serving distinct purposes in the study of data.

Descriptive statistics involves the collection, organization, and summarization of data. This branch focuses on providing a clear and concise overview of a dataset through the use of tables, charts, graphs, and various summary measures, such as means, medians, and standard deviations. The primary objective of descriptive statistics is to describe and present the data in a way that makes it easier to understand the underlying patterns or trends. It is foundational to the practice of statistics because it offers the first glimpse into the data's characteristics, laying the groundwork for more advanced analysis.
On the other hand, inferential statistics extends beyond simply describing the data at hand. It encompasses a range of methods that allow researchers to draw conclusions about a broader population based on the analysis of a sample. Since it's often impractical or impossible to gather data from an entire population, inferential statistics provides the tools to make predictions or generalizations from a representative subset of that population. Techniques such as hypothesis testing, confidence intervals, and regression analysis are commonly used in inferential statistics to make these extrapolations with a quantifiable level of uncertainty. Essentially, while descriptive statistics tells us what the data shows, inferential statistics helps us infer what the data might imply for a larger context.
In this article, we will explore the fundamental statistical metrics necessary to undertake both descriptive and inferential analyses. Understanding these basic metrics is crucial for anyone looking to effectively analyze data, whether the goal is to summarize and describe the data at hand or to make broader inferences about a larger population.
Moments
Moments are fundamental concepts in statistics that help us extract meaningful information from data, going beyond the raw numbers themselves. The true value of data lies not just in the individual data points, but in the insights we can derive from them through various statistical measures, with moments playing a crucial role in this process.
In the context of a random variable, moments are quantitative measures that describe the shape and characteristics of its probability distribution. Essentially, they provide a way to summarize important aspects of the data's distribution, such as its central tendency, variability, skewness, and kurtosis.
The first moment is the mean, which represents the average value of the random variable. It provides a measure of central tendency, indicating where the data tends to cluster.
The second moment is related to the variance, which measures the dispersion or spread of the data around the mean. It gives us insight into how much the data varies.
The third moment concerns skewness, which indicates the asymmetry of the distribution. This helps in understanding whether the data is skewed to the left or right.
The fourth moment deals with kurtosis, which describes the "tailedness" or the peakedness of the distribution, giving us a sense of how much of the data lies in the tails compared to a normal distribution.
By analyzing these moments, statisticians can extract vital information that helps in describing the data's underlying structure, making moments essential tools in both descriptive and inferential statistics.
Expected value
Mathematical expectation, often referred to as the expected value or mean, is a fundamental concept in probability and statistics. For a random variable X, the expectation is denoted as E(X) and is defined as the weighted average of all possible values that X can take, with the weights being the probabilities of those values.
Mathematically, for a discrete random variable X with possible values ( x_1, x_2, … , x_n ) and corresponding probabilities P(X = x_1), P(X = x_2), … , P(X = x_n), the expectation is defined as:

For a continuous random variable, the expectation is given by an integral over all possible values:
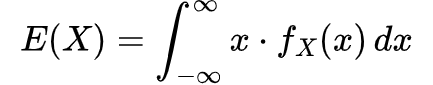
where f_X(x) is the probability density function of X.
The expectation corresponds to the first moment of the random variable. This means that it represents the center of the distribution, providing a measure of the average outcome we would expect if the experiment were repeated many times under the same conditions.
To estimate the expectation or mean μ of a random variable X from a sample of data, we calculate the sample mean. Suppose we have a dataset with n observations x_1, x_2, … , x_n. The sample mean is calculated as:

This sample mean serves as an estimate of the true expected value E(X). It is a simple yet powerful way to summarize the central tendency of the data and is widely used in both descriptive and inferential statistics. By calculating the sample mean, we obtain a single value that represents the average outcome, providing a critical insight into the dataset's overall behavior.
Variance
It is a key statistical metric that quantifies the dispersion or spread of a random variable's values around its mean (expected value). It provides insight into how much the values of a random variable differ from the mean, indicating the degree of variability within the data set.
For a random variable X with an expected value (mean) E(X) = μ, the variance, denoted as Var(X), is defined as the expected value of the squared deviations from the mean:
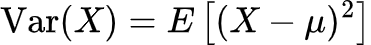
For a discrete random variable, this can be expressed as:

For a continuous random variable, it is given by:
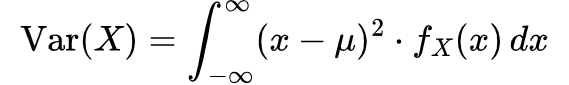
Variance is known as the second central moment because it measures the average squared deviation of each value from the mean, providing a measure of how spread out the values are around the center of the distribution.
To estimate the variance from a sample of data, we calculate the sample variance. Given a dataset with n observations x_1, x_2, … , x_n , the sample variance is calculated as:

Here, n-1 is used in the denominator instead of n to correct for the bias in the estimation of the population variance from a sample, a concept known as Bessel's correction. This adjustment is important because it ensures that the sample variance is an unbiased estimator of the population variance.
The variance provides a critical measure of how much the values in a dataset deviate from the mean, offering insights into the consistency and reliability of the data. A low variance indicates that the data points are close to the mean, while a high variance suggests a wide spread around the mean. Understanding variance is essential for interpreting the variability within data and for making informed decisions based on statistical analysis.
Covariance
Covariance is a statistical measure that quantifies the degree to which two random variables change together. It is a critical concept in understanding the relationship between two variables, particularly when exploring how they vary in relation to each other. Covariance indicates whether an increase in one variable tends to be associated with an increase or decrease in another variable.
Mathematically, for two random variables X and Y, the covariance is defined as the expected value of the product of their deviations from their respective means:
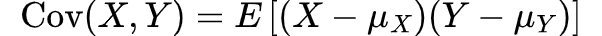
Here, μ_X = E(X) and μ_Y = E(Y) are the means of the variables X and Y, respectively.
For discrete variables, the covariance can be expressed as:

For continuous variables, it is given by:
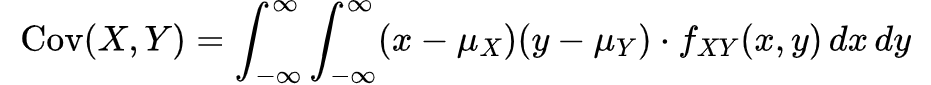
where f is the joint probability density function of X and Y.
Covariance is considered a second-order central moment involving two random variables because it measures the extent to which the variables deviate from their means in a correlated manner. Positive covariance indicates that the variables tend to increase together, while negative covariance suggests that one variable tends to increase when the other decreases. A covariance of zero implies no linear relationship between the variables.
To estimate the covariance from a sample of data, suppose we have two datasets, {x_1, x_2, … , x_n} for variable X and {y_1, y_2, … , y_n}for variable Y, with sample means X and Y, respectively. The sample covariance s_XY is calculated as:

Similar to variance, the denominator n-1 is used to provide an unbiased estimate of the covariance in the population.
Covariance is a foundational measure in statistics for assessing the linear relationship between two variables. It is especially important in fields like finance and economics, where understanding how variables move together is crucial for making predictions and informed decisions. However, while covariance indicates the direction of a linear relationship, it does not provide information about the strength of that relationship, which is where the correlation coefficient comes into play.
Skewness
Skewness (or obliquity) is a statistical measure that describes the degree of asymmetry of a distribution around its mean. It provides insight into the direction and extent to which a dataset deviates from a perfectly symmetrical distribution. Skewness is a standardized third-order moment, meaning it involves the third power of deviations from the mean, which accentuates the impact of extreme values on the measure.

Mathematically, the skewness of a random variable X with mean μ and standard deviation σ is defined as:

This formula expresses skewness as the expected value of the cubed standardized deviations from the mean.
If the skewness is positive, it indicates that the right tail of the distribution is longer or fatter than the left tail, suggesting that the data are skewed to the right (positively skewed).
If the skewness is negative, it indicates that the left tail is longer or fatter than the right tail, implying that the data are skewed to the left (negatively skewed).
A skewness of zero indicates a symmetrical distribution, similar to a normal distribution.
To estimate skewness from a sample of data, consider a dataset with n observations ( x_1, x_2, … , x_n ), where X is the sample mean and s is the sample standard deviation. The sample skewness g_1 can be calculated as:

In this formula:
The term inside the summation represents the standardized deviation of each data point from the sample mean.
The cube of this standardized deviation emphasizes the impact of extreme values on the calculation.
The factor n/((n-1)(n-2)) is a correction factor that ensures the skewness estimate is unbiased, particularly for small sample sizes.
Skewness is an important descriptive statistic because it informs us about the asymmetry in the data, which can have implications for various statistical analyses. For example, many statistical methods assume that the data are normally distributed (symmetrical), so understanding the skewness of your data helps in assessing whether these assumptions hold or if transformations or alternative methods are needed.
Tailedness
It is commonly known as kurtosis[3], a statistical measure that describes the weight of the tails in a probability distribution. It is the standardized fourth-order moment and provides insights into the extremities of the data, indicating how much of the data lies in the tails compared to a normal distribution. In other words, kurtosis helps assess the presence of outliers in a dataset and the sharpness or flatness of the peak of the distribution.
Mathematically, the kurtosis of a random variable X with mean μ and standard deviation σ is defined as:

This formula measures the average of the standardized deviations raised to the fourth power, which gives more weight to extreme deviations from the mean.
A normal distribution has a kurtosis of 3, often referred to as mesokurtic.
If the kurtosis is greater than 3, the distribution is said to be leptokurtic, indicating heavier tails and a sharper peak, meaning more data are concentrated around the mean and in the tails.
If the kurtosis is less than 3, the distribution is platykurtic, implying lighter tails and a flatter peak, meaning the data are more evenly spread out and less concentrated in the tails.
To estimate kurtosis from a sample of data, consider a dataset with n observations ( x_1, x_2, … , x_n ), with X as the sample mean and s as the sample standard deviation. The sample kurtosis g_2 is calculated as:

Kurtosis is an important measure because it gives us a sense of the propensity for outliers in the data. High kurtosis suggests a higher likelihood of extreme values, which can significantly affect statistical analysis and decision-making processes. Understanding kurtosis is crucial when analyzing data distributions, especially in fields where outliers can have a significant impact, such as finance and risk management.
Correlation
Correlation is one of the most commonly used metrics in data analysis, especially when examining the relationship between two variables. It provides a quantitative measure of how strongly and in what direction two variables are related. The most widely used type of correlation is the Pearson correlation coefficient[1], also known as the linear correlation coefficient.
The Pearson correlation coefficient measures the strength and direction of the linear relationship between two variables. Unlike covariance, which is dependent on the units of measurement, Pearson's correlation is a dimensionless measure, meaning it is independent of the scale of the variables. This makes it a versatile and widely applicable metric in various fields of study. It is defined mathematically as:

where:
Cov(X,Y) is the covariance between the two variables X and Y.
σX and σY are the standard deviations of X and Y, respectively.
The Pearson correlation coefficient, denoted as r, ranges from -1 to +1:
An r value of +1 indicates a perfect positive linear relationship, meaning that as one variable increases, the other also increases proportionally.
An r value of -1 indicates a perfect negative linear relationship, where as one variable increases, the other decreases proportionally.
An r value of 0 suggests no linear relationship between the variables.
The Pearson correlation coefficient helps identify two key aspects of the relationship between variables:
1. Direction of the Relationship:
A positive correlation indicates a direct relationship, where both variables tend to increase or decrease together.
A negative correlation indicates an inverse relationship, where one variable increases as the other decreases.
2. Intensity of the Relationship:
Strong correlation: The variables have a high degree of association (closer to |1| ).
Moderate correlation: The association is noticeable but not strong (around |0.5| ).
Weak correlation: The association is low (closer to 0 but not exactly 0).
No correlation: The variables do not exhibit any linear relationship (around 0).
When beginning a bivariate analysis, it is recommended to create a scatter plot. This visual tool helps in assessing the nature of the relationship between the two variables before calculating the correlation coefficient. The scatter plot allows you to see at a glance whether the relationship appears linear, and if so, whether it is positive or negative. This preliminary step is crucial, as the Pearson correlation specifically measures linear relationships, and a scatter plot can reveal whether this assumption is valid for your data.

In summary, correlation, and particularly the Pearson correlation coefficient, is a fundamental metric in data analysis. It not only quantifies the strength and direction of the relationship between two variables but also provides a clear, scale-independent measure that is easy to interpret and apply across various contexts.
Conclusion
This article has covered the key concepts and metrics essential for both descriptive and inferential statistical analysis. We explored the role of data analysis in transforming raw data into meaningful insights and examined core statistical measures, including mean, variance, skewness, kurtosis, covariance, and correlation.
Each metric provides valuable insights: variance and skewness describe data spread and asymmetry, while covariance and correlation reveal relationships between variables, with the Pearson correlation offering a clear measure of linear association.
Understanding and applying these tools allows for more informed, data-driven decisions, forming the foundation of effective statistical analysis.
References
[1] Schober, P., Boer, C., & Schwarte, L. A. (2018). Correlation coefficients: appropriate use and interpretation. Anesthesia & analgesia, 126(5), 1763-1768.
[2] Academia Lab. (2024). Oblicuidad. Enciclopedia. Revisado el 20 de agosto del 2024.
[3] Kurtosis




Comments